Qu'est-ce qu'une représentation objective de la réalité ?
Exemple de la cartographie
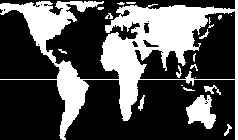
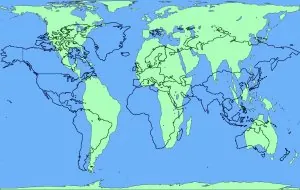
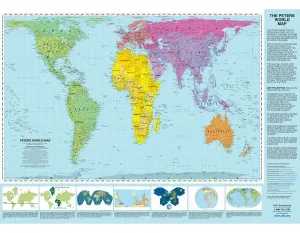
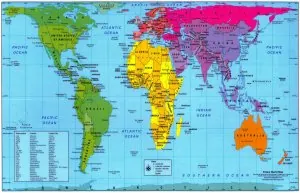
L'une des difficultés majeures de la cartographie a été celle de la projection d'une sphère sur un plan. En résolvant ce problème, le géographe flamand Mercator a réussi à dessiner une première représentation rigoureuse du monde (en 1569). Sa technique consistait à projeter les points du globe terrestre à partir du centre sur un cylindre tangent à l'équateur. Ce cylindre, mis à plat, donne une carte sur laquelle les méridiens sont représentés parallèlement et forment des angles droits avec les parallèles, ce qui est très utile pour calculer la position d'un point par rapport aux pôles et à l'équateur. Cette carte a été la base de la plupart des planisphères depuis quatre siècles. Il existe cependant différentes techniques de projections que l'on peut classifier en fonction des mesures qu'elles permettent de respecter (les angles, les longueurs ou les surfaces). La projection cylindrique classique de Mercator a l'avantage de respecter les angles et donc de faciliter le tracé des itinéraires maritimes et aérien. Mais elle ne respecte pas les surfaces. L'historien et géographe allemand Arno Peters (né en 1916) a inventé une nouvelle projection qui a l'avantage de respecter à la fois les angles et les surfaces, mais qui ne respecte pas les contours.
Quelques thèmes de réflexion
1. Laquelle de ces cartes vous est la plus familière ?
2. Laquelle vous paraît la plus conforme à la réalité ?
3. Voyez où se situe l'équateur sur la carte Mercator classique. Quelle proportion de la surface de la carte occupe l'hémisphère sud ? Quelle est la place de l'Europe sur cette carte ?
4. Sur la carte Mercator classique et sur la carte de Peters, comparez entre-elles les superficies apparentes de l'Europe, de l'Amérique Latine et de l'Afrique. Voici les superficies réelles : Europe : 9,7 M. km2 ; Amérique latine : 17,8 M. km2 ; Afrique : 30,3 M. km2. Que peut-on en conclure ?
5. Quelles conséquenses ont ces distorsions à votre avis ? Faites des hypothèses.
Dans quelle mesure les mappemondes de Mercator et de Peters peuvent-elles prétendre à l'objectivité ? Justifiez votre réponse.
http://www.ac-grenoble.fr/PhiloSophie/logphil/notions/raison/convers/carto/mercator.htm
146239 146240 146241 146242146243
Exemple de la cartographie
L'une des difficultés majeures de la cartographie a été celle de la projection d'une sphère sur un plan. En résolvant ce problème, le géographe flamand Mercator a réussi à dessiner une première représentation rigoureuse du monde (en 1569). Sa technique consistait à projeter les points du globe terrestre à partir du centre sur un cylindre tangent à l'équateur. Ce cylindre, mis à plat, donne une carte sur laquelle les méridiens sont représentés parallèlement et forment des angles droits avec les parallèles, ce qui est très utile pour calculer la position d'un point par rapport aux pôles et à l'équateur. Cette carte a été la base de la plupart des planisphères depuis quatre siècles. Il existe cependant différentes techniques de projections que l'on peut classifier en fonction des mesures qu'elles permettent de respecter (les angles, les longueurs ou les surfaces). La projection cylindrique classique de Mercator a l'avantage de respecter les angles et donc de faciliter le tracé des itinéraires maritimes et aérien. Mais elle ne respecte pas les surfaces. L'historien et géographe allemand Arno Peters (né en 1916) a inventé une nouvelle projection qui a l'avantage de respecter à la fois les angles et les surfaces, mais qui ne respecte pas les contours.
Quelques thèmes de réflexion
1. Laquelle de ces cartes vous est la plus familière ?
2. Laquelle vous paraît la plus conforme à la réalité ?
3. Voyez où se situe l'équateur sur la carte Mercator classique. Quelle proportion de la surface de la carte occupe l'hémisphère sud ? Quelle est la place de l'Europe sur cette carte ?
4. Sur la carte Mercator classique et sur la carte de Peters, comparez entre-elles les superficies apparentes de l'Europe, de l'Amérique Latine et de l'Afrique. Voici les superficies réelles : Europe : 9,7 M. km2 ; Amérique latine : 17,8 M. km2 ; Afrique : 30,3 M. km2. Que peut-on en conclure ?
5. Quelles conséquenses ont ces distorsions à votre avis ? Faites des hypothèses.
Dans quelle mesure les mappemondes de Mercator et de Peters peuvent-elles prétendre à l'objectivité ? Justifiez votre réponse.
http://www.ac-grenoble.fr/PhiloSophie/logphil/notions/raison/convers/carto/mercator.htm
146239 146240 146241 146242146243